Expected value (EV) is a way of calculating how much we stand to make in a particular situation – it can be applied to poker or in lots of areas in real life.
Table Of Contents
- Expected Value Definition
- Expected Value: Real Life Problem
- Expected Value Formula
- Change Variables and Find The Breakeven Expected Value Point
- Expected Value In Poker When Calling
- Expected Value When Betting
- Minimum Defense Frequency
- A Quick Trick To Determine Profitability When Calling
- Expected Value Calculator
- Closing Words
Expected Value Definition
The definition of expected value is the average returns we would expect from taking a particular action (.i.e betting/raising/calling).
The expected value will be based on our current pot equity and pot odds (i.e. opponents bet size) when we face a bet and is based on our equity, our betsize and our oppoents fold frequency when we bet or raise.
If we are the player making the bet, the expected value will be based on our pot equity, bet size and fold equity.
Expected Value: Real Life Problem
To take a real world example – we park our car in a city and unfortunately it costs is $5 an hour. We know we will be at least 1 hour.
We estimate that the probability that we will be caught without a ticket is 10%. The fine for not having a parking ticket is $60.
Should we buy the ticket beforehand?
Or take the chance that we will not be caught?
To solve this problem we can use expected value.
We can find the expected value by using a simple equation. For people who aren't too keen on math, don't worry, it's pretty simple.
To work out our expected value we multiply the potential gain by the probability of that gain occurring (for example saving $5 by not paying the parking ticket by 90%).
Then we must find the product of the potential loss and the probability that the loss will occur and minus this value from the first part.
We have all this information from the real life example above:
Potential gain = $5, Probability of that gain = 100%-10% = 90%.
Potential loss = -$60, Probability of that loss = 10%
The wording may be quite confusing but the expected value formula will make more sense.
Expected Value Formula
Expected value, EV = (probability of gain)*(value of gain) + (probability of loss)*(value of loss)
For our parking ticket example this becomes:
EV = (0.90)*($5) + (0.10)*(-$60) = $4.5 – $6 = -$1.5
So on average, every time we don't pay our parking ticket we will stand to lose $1.5.
This may confuse people as in no single case can we lose $1.5 – we either save $5 or we have to pay $60.
The $1.5 comes from is the average loss we will make over a long period of time. So if we did this 100 days in a row, 90 of the days we would have saved $5 each day for $450, but we would have been fined 10 times for $600 total.
Thus on average, we would have lost $150 which is $1.5 per day.
Change Variables and Find The Breakeven Expected Value Point
Using this simple calculation we can see how changing the variables affects our expected value; if it is less likely we will be caught and fined we should not pay for the ticket, that is obvious. For example, it is 1% likely that we will be caught without a ticket:
EV = (0.99)*($5) + (0.01)*(-$60) = $4.95 – $0.6 = $4.35. Therefore it makes sense to not buy a ticket for these parameters.
Intuitively that makes sense too since it is so unlikely we will have to pay $60 dollars.
If the fine cost less or the cost of parking cost more, that will increase the EV of not buying a ticket.
We can also find the point at which it becomes profitable to start not paying for tickets.
We find the breakeven point by setting the EV to zero and then find the probability that we will be caught which we have labelled as X.
This is called the breakeven point (requires some algebra):
EV = 0 = (x)*($5) + (1-x)*(-$60) => 5x-60 + 60x = 0
Therefore: 65x =60 and x = 60/65 = 92.3%.
So if we are likely to be caught greater 7.7% of the time we should buy a ticket; and if less than that we should not buy a ticket.
We can also apply this analysis to poker in situations where we know our equity pot odds, bet size and pot size.
Expected Value In Poker When Calling
To go back to the previous hand example with A9 of diamonds we had pot odds of 28% and we had pot equity of 18%. The pot odds are based on how much he bet and pot equity is based on the hands we assumed he would be bluffing with. So let’s put that all together to do an expected value calculation.
Again the expected value will be:
EV = (probability of gain)*(value of gain) + (probability of loss)*(value of loss)
The probability of gain will be our equity which is 18%.
The probability of loss will be 1-equity which is 82%.
The value of our gain will be $67.5 and the value of our loss is -$26. Subbing in:
EV = (0.18)*(67.5) + (0.82)*(-$26) = 12.15 – 21.32 = -$9.17
Therefore this will be an unprofitable call to make. That should also be intuitive since we are winning so infrequently.
Expected Value When Betting
Here is another example of when betting on the river.
We opened to 3bb from UTG and got one call from the Button. On the flop of 9h7s3s, we have an inside straight draw and two overcards so we decide to continuation bet the flop and 3c turn.
Now on the river, we have to decide whether to bet again.
Firstly we can assume that we will lose if we check this river. We only have Jack high and unless our opponent has a busted draw AND checks, we will not take this pot down.
Therefore, checking has an EV of close to zero.
So what is the expected value of betting?
Well, we need to know:
- Our bet size = $32
- The pot size before our bet = $42.5
- How often our opponent calls = ?
How often our opponent calls is dependent on a lot of factors, but taking a rough estimate, let's say he will fold 50% of the time since we have shown a lot of strength and the river is a scare card.
We then the expected value equation becomes:
EV = (probability of gain)*(value of gain) + (probability of loss)*(value of loss)
EV = (0.5)*($42.5) + (1-0.5)*(-$32) = $5.25
Therefore, betting $32 is going to be very profitable in this spot if our opponent folds 50% of the time – the reason for that: our opponent is folding too much.
He should be calling at least 57% of the time to prevent us from making an immediate profit according to the minimum defence frequency formula which we will cover in the next section.
EV = (0.43)*($42.5) + (1-0.43)*(-$32) = ~$0
This J♦T♦ example is quite simple because we are on the river and there is only one more betting round to play.
However, it gets way more complicated when trying to estimate EV on the flop or turn for a number of reasons:
- You don't know what cards will come on the turn or river
- You don't know how your opponent will react to each of these cards
- There are so many different ways the hand can be played out, it's almost impossible to work out each path by hand.
For that reason, simple EV calcs like this are usually only performed on the river and software such as Cardrunners EV is used to simulate multiple street EV bets. Although these simulations take a lot of time to set up.
Minimum Defense Frequency
As mentioned, the minimum defence frequency is how often our opponent should call our bet to prevent us from making an immediate profit.
We can work our opponent's minimum defense frequency using this formula:
MDF = pot size / (pot size + bet size)
For the last example:
MDF = $42.5 / ($42.5 +$32) = 0.57 or 57%
Notice that increasing our bet size, decreases how often our opponent should call.
And the opposite is true too: decreasing our bet size increases how often our opponent should call.
A Quick Trick To Determine Profitability When Calling
A quick way to determine the profitability of a call without doing a full EV calculation is to compare the pot odds and our equity.
In the case of the example hand, we have pot odds of 28% and we have equity of 18%. If the equity is less than the pot odds we should not call as it would be unprofitable; conversely if we had more than 28% equity we can make the call as it would be profitable to do so.
You are not expected to do these calculations in their head while at the poker table. The purpose of the calculations is to analyse difficult hands off the table after your poker session, not during a game. This allows you to determine if you made the right decision and correct mistakes.
One of the main drawbacks of EV calculations is that you cannot perform them before the river as there are so many variables at play. We do not know what our opponent will do on future streets, will he check or will he bet? What card will come on the turn and river? If he does bet, what size will he use?
This is what makes poker such a complex game and a difficult one to solve computationally.
Despite this fact, expected value, pot odds and equity are useful in both poker and real life. So it is worth taking the time to understand how it is applied.
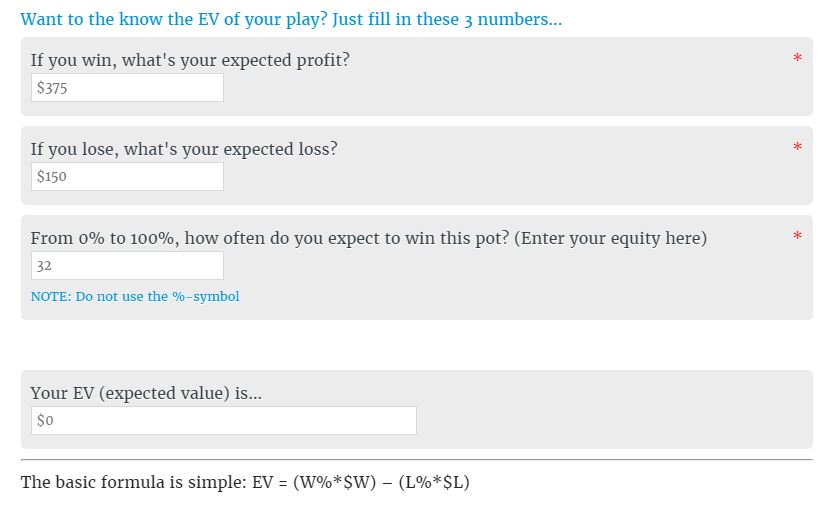
Expected Value Calculator
Make sure you check out this expected value calculator over at RedChip Poker:
It is extremely easy to use. All you have to type in are the three values in the above fields and it returns the expected value of that particular situation.
Here is a video which recaps the main points we covered in this lesson:
Closing Words
So that's it for our lesson on Expected Value. You should have already worked through the counting outs, pot equity and pot odds lessons before doing this so if not make sure you check them out.
You should now have a much better understanding of the math behind poker – your next step is to put it into practice and perfect it. Good luck!
Head back to poker 101 to learn more or check out the blog page for blog updates.